Problem #5 Solution
First, we show that the streamless sets are closed under adding one new element:
Lemma streamless_plus_one : forall X, streamless X -> streamless (unit + X).
Suppose that f : nat -> unit + X. WLOG, we can assume that f 0 or f 1 = inr x0 for some x0 : X (look at f 0 and f 1; if both are inl tt then we are done). We can then transform f into a sequence hat x0 f : nat -> X by sending any unit elements to x0.
Now, we can use the fact that X is streamless to find two elements 1 < i < j such that hat x0 f i = hat x0 f j. We can now check f i and f j; if both are inl tt or both are inr x for some x then we are done. The only case to consider is if f i = inl tt and f j = inr x. Since hat x0 f i = hat x0 f j, this implies that x = x0 so we can take j and 0/1 (whichever one gave the value inr x0) as our pair of distinct numbers.
Now we can prove our main theorem. Suppose f : nat -> X + Y. We will let hat_l f : nat -> unit + X and hat_r f : nat -> unit + Y denote the obvious functions which “forget” all right (resp. left) elements of the sequence f.
Using the previous lemma applied to hat_l f, we can find a pair of numbers i_0,j_0 such that hat_l f i_0 = hat_l f j_0. By looking at the “tail” of f past i_0,j_0 we can find a new pair i_1,j_1; and repeating this process, we can via recursion define a subsequence which lists the i’s produced by this process.
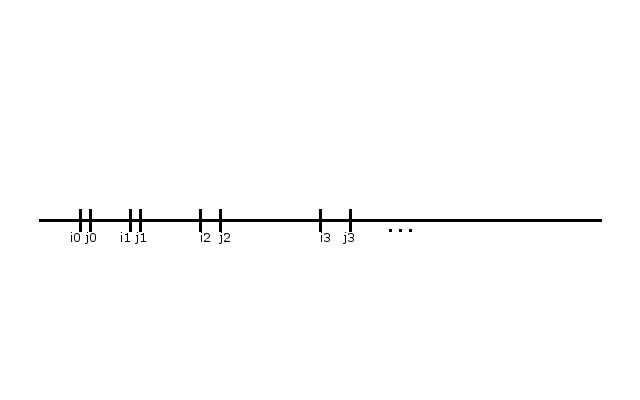
The basic idea
Now, using the streamlessless of unit + Y, we can find i_k and i_l whose values match when forgetting the X values. Now check f i_k and f i_l; if they are both Y elements we are done. Thuse suppose one of them (WLOG i_k) is an X value; by virtue of the way the sequence of i’s was generated, we can use i_k and j_k as our pair of distinct numbers.