Problem #1 Template

Let f : nat -> nat be a decreasing function. Here, we mean decreasing in the non-strict sense (and indeed, no strictly decreasing functions nat -> nat exist).

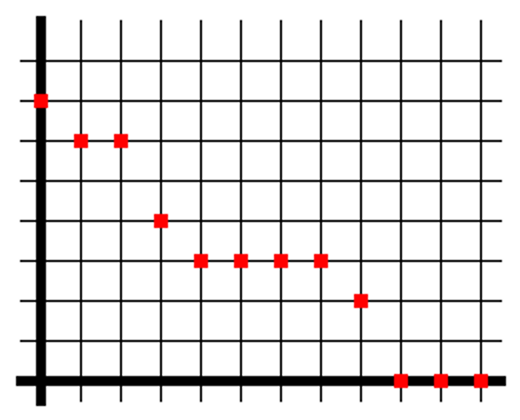
Your typical decreasing function

Classically, we can prove that f must eventually be constant, i.e. there is a position after which the value of f never changes. Unfortunately, this cannot be proven constructively (we will revisit this in Problem #2), but we can prove something weaker. By an n-valley, we will mean a sequence of n+1 consecutive points that have the same value. For example, in the above figure, there is a 3-valley at position x=4.

Problem: Show that for any decreasing f and natural number n, there is an n-valley somewhere in f.